Fractal tree

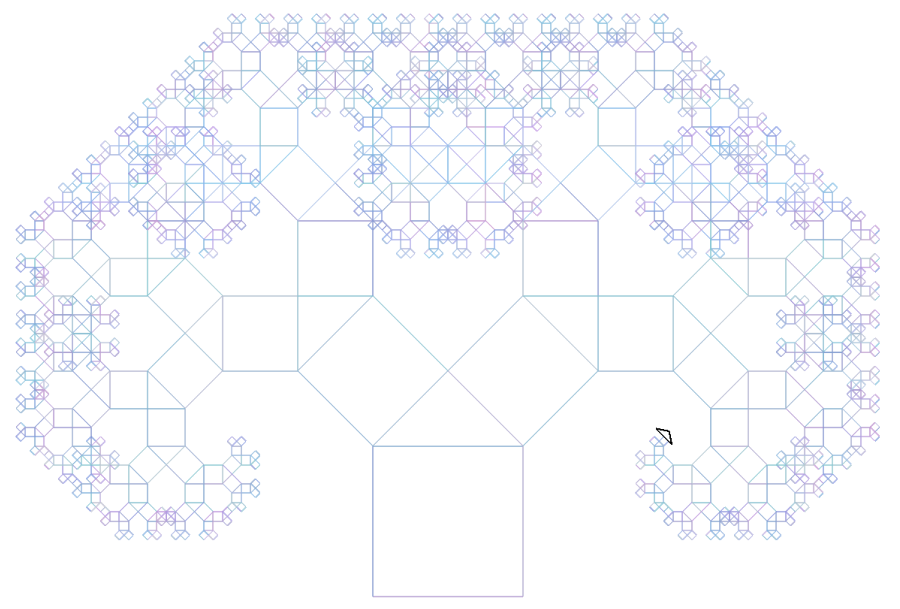
Lets create the factorial tree with a turtle library. Making the factorial tree allows us to demonstrate how this library is drawing amazing images in an easy way.

Preparation

Creating the project.

cargo new factorial_tree --bin

Adding dependency in cargo.toml.

[dependencies]
turtle = "^1.0.0-alpha.8"

Coding in src/main.rs

We need to import the turtle crate.

extern crate turtle;

use turtle::{Turtle, Point, Color};

Lets create the turtle in the main function.

fn main() {
    let mut turtle = Turtle::new();

    // setting the speed of the turtle
    turtle.set_speed(10);
}

Our tree is a fractal which consists of 1 large square and 2 small squares. Every small square represents itself the large square of the next level.

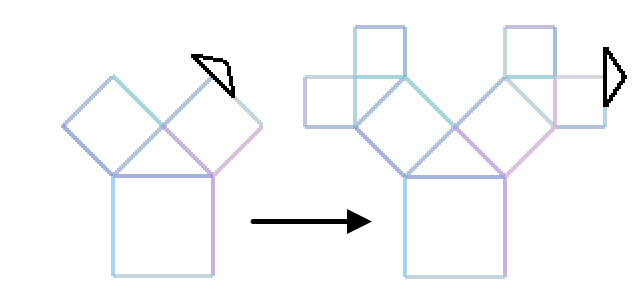
We can use the recursion. Lets create the draw function.

fn draw(turtle: &mut Turtle, side: f64, depth: usize) {
    // Draw the large square from left upper corner
    for _ in 0..4 {
        turtle.right(90.0);
        turtle.forward(side);
    }

    // Draw the small squares
    // ...
    }
}

This function accepts 3 parameters: the turtle object which was created in the main function; the size of the first large square's side; the depth of recursion (it's a size of the tree).

We need to check the actual depth for drawing smaller squares. Then we can move to the left upper corner of every small square and call the draw function.

// If you need to draw a smaller level
if depth > 0 {
    // The side of the small square
    let smaller_side = side / f64::sqrt(2.0);

    // Move to the starting position of the left small square
    turtle.pen_up();
    turtle.left(45.0);
    turtle.forward(smaller_side);
    let position = turtle.position();
    turtle.pen_down();

    // Remember the heading
    let heading = turtle.heading();

    // Draw the left small square
    // It's the large square on the next level/depth
    draw(turtle, smaller_side, depth - 1);

    // Restore the heading
    turtle.set_heading(heading);

    // Return to the starting position of the left small square
    // Move to the starting position of the right small square
    turtle.pen_up();
    turtle.go_to(position);
    turtle.right(135.0);
    turtle.forward(side);
    turtle.left(45.0);
    turtle.forward(smaller_side);
    turtle.pen_down();

    // Draw the right small square
    // It's the large square on the next level/depth
    draw(turtle, smaller_side, depth - 1);
}

Now we need to change our main function.

fn main() {
    let mut turtle = Turtle::new();
    turtle.set_speed(10);

    // The side of the first large square
    let side = 50.0;

    // Draw the tree
    draw(&mut turtle, side, 3);
}

But as our tree is made in the black color we can make it look more attractive and change the color of our tree by adding a new function.

/// Returns the color by the position of the turtle
fn get_color(position: Point) -> Color {
    Color {
        red: 130.0 + f64::abs(position[0] % 75.0),
        green: 150.0 + f64::abs(position[1] % 55.0),
        blue: 210.0 + f64::abs(position[1] % 25.0),
        alpha: 0.8
    }
}

Now we need to change the code which drawing the large square.

// Draw the large square
    for _ in 0..4 {
        // Get position for setting color
        let position = turtle.position();
        // Each side has a different color
        turtle.set_pen_color(get_color(position));

        turtle.right(90.0);
        turtle.forward(side);
    }

Souce code on GitHub

Bonus

It's a tree with 9 level of depth.